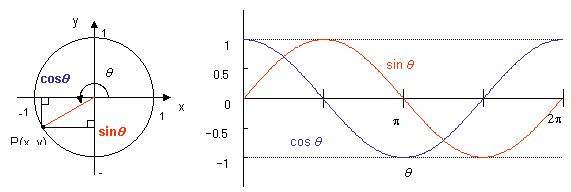
図3.1 三角関数
ここでは,代表的な関数などの数学的な基本概念を復習し,数値計算での表し方を解説します.
三角関数は,図3.1のような単位円上で一般角θを考えた場合,点Pのx,y軸への投射として表されます.

複雑な形の信号は,簡単な三角関数の和として表すことができ,各成分ごとに解析することができます.逆に,三角関数を合成することで,さまざまな形の信号を作ることができます.
正弦関数は,三角関数の基本となる関数です.関数の特徴として,
などがあげられます.
なお,関数は,独立変数(例えばx)と従属変数(例えばy)との関係を表しますが,物理現象を表す場合は独立変数が時間となったものと考えられます.つまり,時間による現象の変化が関数の関係で表されることになります.
余弦関数は,正弦関数を90[deg](p/2[rad])進めたものです.特徴としては,
などがあげられます.
なお,余弦関数と正弦関数は,位相がずれている以外は関数の形が同じです.そのため,特に基準(時間の原点など)を考えない場合は,正弦関数として考えます.
演習3.1(解答例)
(1) 新しいBookを開き,sheet1の名称を「三角関数」に変更し,1行目A列から,次の文字を入力しなさい.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | step | x [rad] | sin(x) [rad] | cos(x) [rad] |
(2) A2より,初期値0,刻み1の200個の連続データ(A202まで)を作成しなさい.
(3) 0~2πの値を200分割して計算するため,B2に【= A2*PI()/100】を入力し,B202までコピーしなさい.
(4) B列の値を参照して,C列,D列に式を入力しなさい.
(5) C列,D列のデータを折れ線グラフで表示しなさい.
(6) 上のグラフをそれぞれ2周期分表示するようにデータを変更しなさい.
演習3.2(解答例)
正弦波の信号入力に対し,図3.2の回路で示される半波整流信号の波形を4周期まで表示しなさい.ただし,x,sin(x)の値は,演習3.1のデータを使うこと.

ヒント:
整流回路があるため,正弦波のマイナスの電流が流れません.したがって,正弦波の負の部分のない波形となります.これを表すためには,IF関数,
IF(条件式,引数1,引数2)
[条件式が真のとき引数1を返し,偽のとき引数2を返します]
を利用します.
(1) 「三角関数」のシートをコピーし「半波整流信号」に名称変更する.
(2) B2の式【= A2*PI()/100】を【A2*PI()/25】に変更し,B202までコピーする.
(3) E2に,【= IF(C2 > 0, C2, 0)】を入力し,E202までコピーする(E列の見出しは適宜入力).
(4) E列のグラフを表示する.
演習3.3(解答例)
次の式のように正弦波を合成し,波形をグラフ表示しなさい.
y = (4/π) { sin x + (1/3) sin 3x + (1/5) sin 5x + (1/7) sin 7x }
ヒント:
各項を個別に計算し,その和をとります.
(1) シート「三角関数」をコピーし,「合成波」に名称変更する.
(2) D列を削除する.
(3) D2に【= sin(3*B2) / 3】を入力する.
(4) 同様に,E2・F2にもB2を参照して3・4項の式を入力する.
(5) G2に【= 4 * sum(C2:F2) / PI()】を入力し,G202までコピーする.
(6) D2からG202までを選択し,下方向に連続コピーする.
(7) G列の選択範囲をグラフ表示する.
一定の割合で増減する現象は,べき乗関数y = axによって表されます.べき乗関数とは,独立変数xがべき乗についている関数です.べき乗関数を微分すると元のべき乗関数に係数をかけた相似な関数が得られます.この係数が1になる a の場合を指数関数 y = ex といいます.ここで,eは,自然対数の底あるいはネピア(Napier)の数とよばれ,
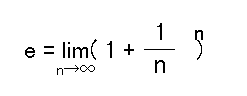
で定義されます.その値は,2.71828182845904・・・という無理数です.また,eの値は,次式で示す無限級数で展開することができ,
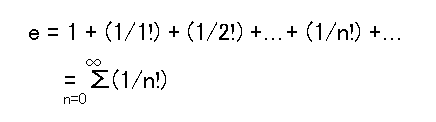
によって求めることができます.
対数関数は,
y = xn
であるとき,
n = logx y
と表現し,xを底とするyの対数はnであると定義します.底をeとする自然対数はln x,底を10とする常用対数はlog xで表します.特に明示する必要があるときは,底を表示します.指数関数y = exの逆関数がy = ln xであり,y = xに関して線対称になっています.
演習3.4(解答例)
次の手順に従って,eの値を,極限,無限級数の式を使ってそれぞれ求めよ.また,表計算ソフトの関数【=EXP(1)】を入力したときの値と比較しなさい.
(1) sheet2の名称を「ネピア数」に変更し,A列1行目から次の文字を入力しなさい.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | n | lim(1+1/n)^n | n | 1 |
(2) A2に【1】を,A3に【= A2 * 100】を入力し,A3の式をA9までコピーしなさい.
(3) B2に【= (1 + 1/A2)^A2】を入力し,B9までコピーしなさい.
(4) D2~D21に,1~20の連続データを入力しなさい.
(5) E2に【= E1 * (1/D2)】を入力し,E21までコピーしなさい.
(6) F1に【= SUM(E1:E21)】を入力しなさい.
(7) F3に【= EXP(1)】を入力しなさい.
演習3.5(解答例)
0.05 ≦ x ≦ 2.5における指数関数,対数関数のグラフを作成しなさい.ただし,xの刻みを0.05とする.
ヒント:
(1) sheet3の名称を「指数・対数関数」に変更する.
(2) A1から次の文字を入力する.
| A | B | C | |
|---|---|---|---|
| 1 | x | e^x | ln(x) |
(3) A2より,刻み幅0.05で0.05~2.5までの50個の連続データ(A51まで)を作成する.
(4) A列のデータを参照して,それぞれB,C列を入力する.ただし,指数関数,対数関数には表計算ソフトのEXP(),LN()をそれぞれ用いる.
(5) B列,C列のデータを折れ線グラフで表示する.
関数を微分することによって,その関数の増減,極大・極小といった特徴や性質を知ることができます.微分については,すでに学んだと思いますが,これを計算機で表すにはどうしたらよいでしょうか.
例えば,
f(x) = xn → f'(x) = nxn-1
f(x) = sin(x) → f'(x) = cos(x)
のように関数が数式で表されている場合,微分後の式を直接プログラム中に書くことも可能です.しかし,シミュレーションや実験から得られるような連続データや数表,あるいは複雑な数式の場合はどうでしょうか.このような任意の関数の場合,直接微分できないことも考えられます.
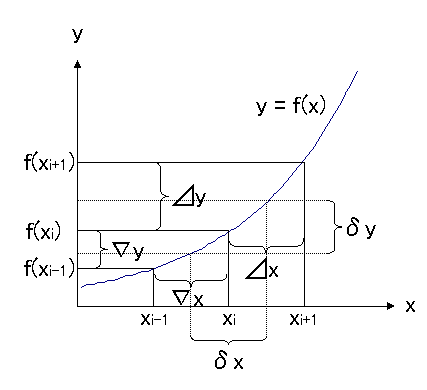
ここで,微分の定義を振り返ってみましょう.関数のある点xiでの接線の傾き(微分係数,変化率)は,
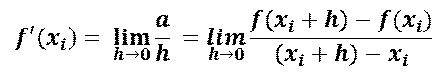
のように表されます(図3.3).
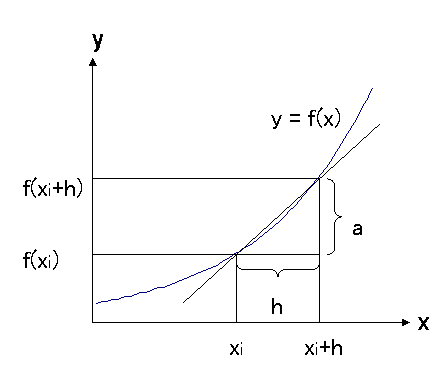
この各点での微分係数を,xiに対応して並べた関数f'(x)が導関数であり,微分とはこの導関数を求めることです.今,
Δ x = h
Δ y = a = f(x+h) - f(x) = f(x + Δ x) - f(x)
とすると,導関数は,
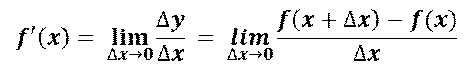
と表されます.
ここで,導関数の式を眺めて見ましょう.この式から,xおよびyの微小区間の差Δ x,Δ yを取り,その間隔を十分小さくすれば,Δ y / Δ x が微分の近似として利用できそうです.
このように,任意の関数の微分を求める数値計算は,xおよびyの十分に微小な区間の差(差分)を取り,その商(差分商)を計算することで近似します.
差分のとり方には,
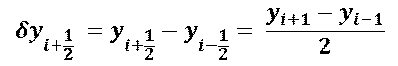 ]
]
があります(図3.4).前方差分,後方差分は添字の付け方が異なるだけで,値は同じものです.
Δ yi = ∇ yi+1
∇ yi = Δ yi-1
中心差分は,前後のデータの中点(平均値)を利用する方法で,精度が高くなります.しかし,yi+1/2やyi-1/2などの値が計算できない場合もあるため,次のようなスターリングの差分を用います.
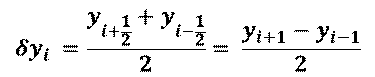
通常はデータの刻み幅を細かくすることでよい近似値を得ることができます.
また,高階の微分も同様に,差分をn階とることで近似できます.つまり,n階の微分dny/dxnは,n階の差分商 Δ ny / Δ xnで近似できます.
1階後方差分商による1階微分の近似
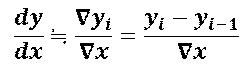
2階後方差分商による2階微分の近似
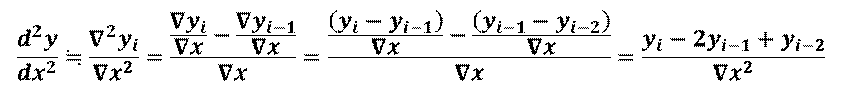
3階後方差分による3階微分の近似
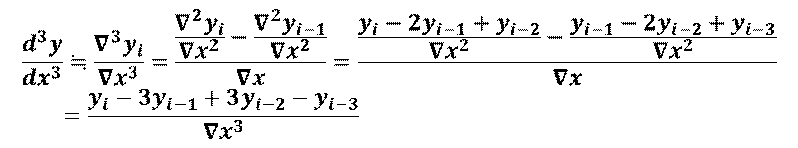
n階後方差分商によるn階微分の近似
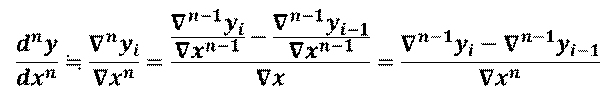
例題3.1
二次関数 y = x2を例に微分と差分商を比較しなさい.
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.
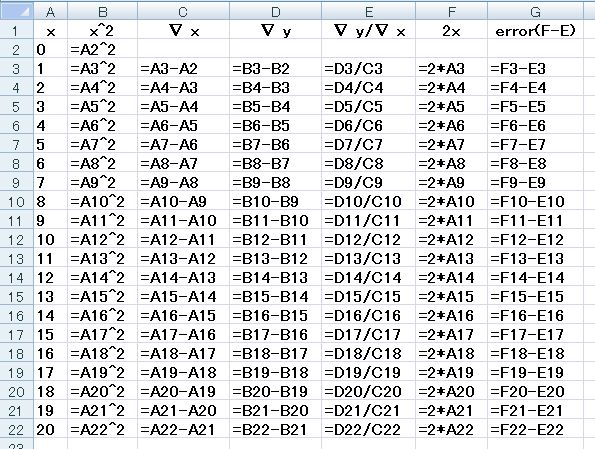
演習3.6(解答例)
同様に,sheet2に指数関数e^xの1階微分を差分を使って表し,グラフに表示しなさい.ただし,xの範囲は0~1で刻みは0.01とする.
演習3.7(解答例)
次の手順に従って,三角関数 y = sin(x) の微分と差分商を比較しなさい.
(1) sheet3に次の文字列を入力しなさい.
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | n | x | sin(x) | ∇ y/∇ x | δ y/δ x | cos(x) | error(F-D) | error(F-E) |
(2) nを0から1刻みで200まで入力し,B2に【=A2*PI()/100】を入力し,B202までコピーしなさい.
(3) B列を参照し,C~Hまでの列を入力し,誤差を比較しなさい.また,C,D,E,F列をグラフ表示しなさい.
(4) 2階の後方差分商をI列に作りなさい.
(5) I列をさきほどのグラフに付け加えなさい.
積分は,微分の逆の演算です.関数F(x)の導関数がf(x)のとき,すなわち
F'(x) = f(x)
が成り立つときF(x)をf(x)の不定積分または原始関数といい,不定積分を求めることをf(x)を積分するといいます.
しかし,f(x)の不定積分が必ずしも数学的に求められない場合でも,数値積分によって積分値の近似値を求めることができます.
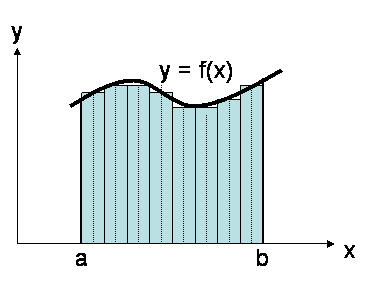
区分求積法は,図3.5左図に示すように関数f(x)のある区間[a, b]の積分を求める場合,図3.5右図のように一定幅の短冊に区切り,各短冊の面積を計算しそれらを足し合わせる方法です.つまり,
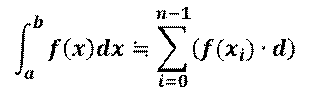
によって近似的な面積を求めます.
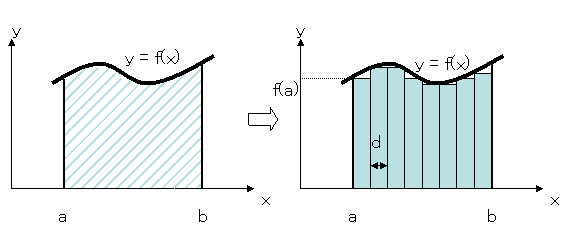
例題3.2
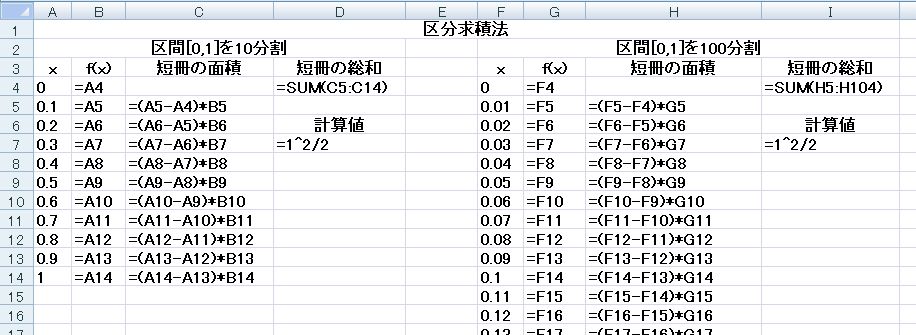
f(x) = xの区間[0,1]の積分を,xをそれぞれ10分割,100分割した区分求積法で求めたい.
(1) 前述の式を参考に,f(x)およびdに式および値を入れた近似式および漸化式を求めなさい.
(2) (1)の近似式に基づき,表計算ソフトを用いて数値計算を行い,近似値を求めなさい.また,数学的に求めた積分値と区分求積法で求めた近似値を比較しなさい.
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.
演習3.8(解答例)
単位円の面積を区分求積法で求めたい.
(1) 単位円の方程式(x2 + y2 = 1)を用いて,区分求積法の近似式および漸化式を求めなさい.ただし,d=0.1とする.
(2) (1)の漸化式に基づき,表計算ソフトを用いてy ≧ 0の範囲で0 ≦ x ≦ 1まで数値計算し(1/4単位円の面積),それを4倍して単位円の面積を求めなさい.また,求められた面積をPI()の値と比較しなさい.
(3) (2)と同様の範囲で,d=0.01としたときの面積を求めなさい.また,求められた面積をPI()の値と比較しなさい.
中点法は,f(x)の値を短冊の中央値として計算する方法です(図3.6).これにより,短冊の端で面積を計算するよりも誤差が少なくなります.
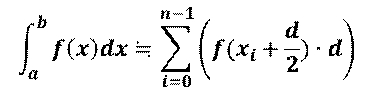
演習3.9(解答例)
演習3.8 (1)~(3)の内容を,中点法を用いて確かめなさい.
区分求積法と同様に,関数f(x)の区間[a,b]をn等分して小区間に分けますが,近似を行うために,短冊ではなく各等分点における関数の値を直線で結んで小区間ごとに台形を作り,これを足し合わせるようにします.
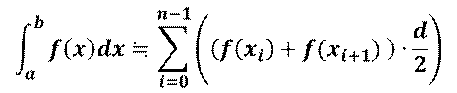

演習3.10(解答例)
演習3.8 (1)~(3)の内容を,台形法を用いて確かめなさい.
関数の直交性という概念は,フーリエ級数などを理解するうえで重要です.いま,平面内の2つのベクトルA,Bを考える.A,Bが角度θで交差しているとき,その内積Cは,
C = |A|・|B|・cosθ
で表され,C = 0,つまり,cosθ = 0 (θ= π/2)のとき,AとBは直交します.
このベクトルの直交の概念を関数に当てはめると,「ベクトルの内積」に相当するのが「定義域内で2関数の積を積分すること」です.したがって,
C =∫ f(x)・g(x) dx = 0
であれば,関数f(x)とg(x)は直交することになります.
演習3.11(解答例)
定義域[0, 2π]において,sin(x)とcos(x)が直交することを確かめたい.
(1) 区分求積法を用いた場合の近似式と漸化式を求めなさい.ただし,定義域を200分割することとする.
(2) (1)の漸化式に基づき,表計算ソフトを用いて関数の直交性を確かめなさい(つまり,積分値が十分0に近ければよい).