
図4.1
代表的な数値計算法の理論として非線形方程式の根を求める方法を取り上げます.実際の実験などで非線形方程式の根を単順に求めるような問題を扱うことは少ないのですが,数値計算の考え方を理解する基礎として重要です.
数値計算は,2章で説明したとおり,問題を定式化し,漸化式を作り,数値を参照しながら反復計算を行い,許容誤差範囲内で近似値を決定することが基本となります.ここでは,表計算ソフトを使って容易に実行が可能なものをとりあげましたが,数値計算法には数多くの方法論があり,全てを紹介できないので,各自学習してください.非線形方程式の他にも,連立線型方程式や行列,微分方程式などの演算を数値計算で行うことができ,これらについては,後半のプログラミングで取り上げます.
また,最後に,表計算ソフトを利用したシミュレーションについて事例を挙げます.
4.1.2 ニュートン・ラフソン法 (Newton-Raphson)
非線型方程式 f(x) の根は,
f(x) = 0
で与えられます.これは,関数 f(x) と x 軸の交点を求めることに他なりません.数値計算による根の求め方にはいくつかありますが,ここでは「2分法」と「ニュートン法」について説明します.いずれも,反復計算を行い根に収束する近似値列 x1,x2,x3,...,,xk,を求め,適当な k で停止させ近似値 xk を求める方法です.
近似値の判定基準は,「誤差基準」もしくは「残差基準」で行います.誤差基準では,根αに対し誤差 ek = xk - α の絶対値があらかじめ決められた許容誤差 ε (> 0) より小さいとき近似値とします.残差基準では,残差 rk = f(xk) の絶対値が許容残差 ε (> 0) より小さいとき近似値とします.残差基準では,必ずしも近似値が根 α に近いとは限らないため,誤差基準のほうが近似値の誤差評価としては正しいですが,実用上残差基準で適応できる例も多いため両者とも重要です.

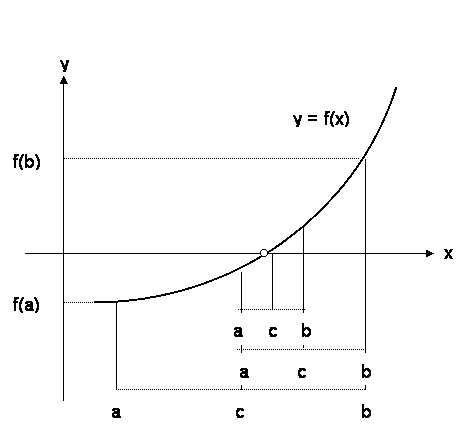
2分法は,根の存在する範囲を順次狭めていき根に収束させる「直接探索法」です.近似値への収束に多少時間がかかりますが,厳密な誤差評価を行うため,よい近似値を得られます.
2分法は,非線型方程式 f(x) = 0 の閉区間 [a, b] において,
f(a) ≦ 0 ≦ f(b),もしくは,f(b) ≦ 0 ≦ f(a)
であれば,区間 [a, b] の間に f(x) = 0 の根 α が存在するという原理を用います.計算方法は次のようになります.
例題4.1 2分法による計算
次の方程式の根を2分法により求めなさい.ただし,区間の初期値は,[1, 3] とする.また,得られた根を 3 の平方根と比較しなさい.
f(x) = x2 - 3 = 0
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.

演習4.1 2分法による計算(解答例)
(1) 次の方程式の根を2分法により求めなさい.ただし,区間の初期値は,[1, 3] とする.また,得られた根を5の3乗根と比較しなさい.
f(x) = x3 - 5 = 0
(2) 次の方程式の根( > 0 )を2分法により求めなさい.ただし,区間の初期値は,[0, 5] とする.また,得られた根を数学的な解と比較しなさい.
f(x) = x2 + x - 6 = 0
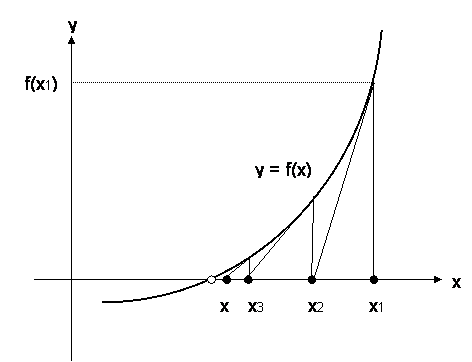
ニュートン・ラフソン法(ニュートン法)は,導関数を利用して,適当な初期値から反復計算を行い根に収束させる「逐次近似法」です.
図4.3に示すように,非線形方程式
y = f(x)
の x1 における接線の傾き m は,接線と x 軸との交点を x2 とすると,
m = f(x1) / (x1 - x2)
と表されます.これを x2 について解くと,
x2 = x1 - f(x1) / m
となります.
一方,x1 における接線の傾き m は,f(x) の導関数f '(x)とすると,
m = f '(x1)
です.したがって,x2 は,
x2 = x1 - f(x1) / f '(x1)
と求められます.
上式を一般化すると,
xk+1 = xk - f(xk) / f '(xk)
となります.これを適用して反復計算を行い,xk - xk+1 が許容誤差範囲内となったところで近似値とします.
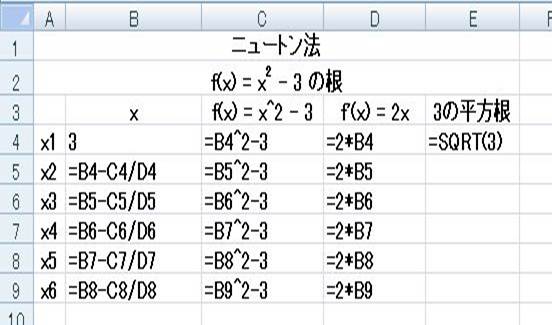
例題4.2 ニュートン法による計算
次の方程式の根をニュートン法により求めなさい.ただし,初期値 x1 = 3 とする.また,得られた根を 3 の平方根と比較しなさい.
f(x) = x2 - 3 = 0
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.
演習4.2 ニュートン法による計算(解答例)
(1) 次の方程式の根をニュートン法により求めなさい.ただし,初期値 x1 = 3 とする.また,得られた根を5の3乗根と比較しなさい.
f(x) = x3 - 5 = 0
(2) 次の方程式の根( > 0 )をニュートン法により求めなさい.ただし,初期値 x1 = 5 とする.また,得られた根を数学的な解と比較しなさい.
f(x) = x2 + x - 6 = 0
ニュートン法は,導関数の計算を行わなければならないため,プログラム上負担となります.そこで,ニュートン法の導関数部分を差分商の近似で置き換えたものが割線法です.割線法の式は,次のようになります.
xk+1 = xk - { (xk-1 - xk)・f (xk) / ( f (xk-1) - f (xk) ) }
例題4.3 割線法による計算
次の方程式の根を割線法により求めなさい.ただし,初期値は,(x1, x2) = (3, 2) とする.また,得られた根を 3 の平方根と比較しなさい.
f(x) = x2 - 3 = 0
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.

演習4.3 割線法による計算(解答例)
(1) 次の方程式の根を割線法により求めなさい.ただし,初期値は,(x1, x2) = (3, 2) とする.また,得られた根を5の3乗根と比較しなさい.
f(x) = x3 - 5 = 0
(2) 次の方程式の根( > 0 )を割線法により求めなさい.ただし,初期値は,(x1, x2) = (5, 4) とする.また,得られた根を数学的な解と比較しなさい.
f(x) = x2 + x - 6 = 0
電気回路ではさまざまな波形の信号を取り扱いますが,その信号を解析するためには,どのような周波数成分から成り立っているかを調べることが重要です.それには,信号の波形から周波数の分布を計算しなければなりません.この計算に利用されるのがフーリエ級数,フーリエ変換です.
3次元空間での任意の点へのベクトルは,互いに直交する3軸(x, y, z)の各軸方向の単位ベクトルi, j, kを用いて,
r = a・i + b・j + c・k
と表されます.同様に,n次元空間における任意の点へのベクトルは,互いに直交するn個の軸の各軸方向の単位ベクトルf1, f2, f3, …, fnを用いて,
r = a1・f1 + a2・f2 + … + an・fn = ∑ ai・fi (i = 1~n)
と表すことができます.ここで,各単位ベクトルは直交していることから,
fi・fj = 0 (i≠j)
です.このことから,任意のベクトルは互いに直交する単位ベクトル成分に係数をかけたものを足し合わせることで表現できることがわかります.
この概念を関数に拡張すると,任意の関数は互いに直行する関数に係数をかけたものを足し合わせることによって表現できることになります.前回の関数の直交性で確かめたとおり,三角関数sinおよびcosは互いに直交する関数です.したがって,任意の関数は,sinおよびcosに係数をかけたものを足し合わせることで表現することができることになります.つまり,
F(x) = (a0/2) + ∑ (an・cos(n・x) + bn・sin(n・x)) (n = 1~∞)
となります.これをフーリエ級数といい、上式をフーリエ級数展開といいます.また,各係数an,bn (n = 1~∞)をフーリエ係数といいます.フーリエ級数の各成分a0, an, bnは,
a0 = (2/T)∫f(x) dx
an = (2/T)∫f(x)cos(n・x)dx
bn = (2/T)∫f(x)sin(n・x)dx
で表されます.
このことは,フーリエ級数によって,任意の関数(信号)を作ることが可能であるとともに,ある信号をフーリエ級数に展開しフーリエ係数を求めることで,その信号がどのような周波数成分から成り立っているか求められることを表しています.
フーリエ級数を複素指数関数表現にしたものがフーリエ変換であり,時間関数を周波数関数へ変換します.また,周波数関数を原関数である時間関数へ戻すことをフーリエ逆変換といいます.実用的な計算ではフーリエ変換を計算することはあまりなく,フーリエ級数を用いて関数の合成やフーリエ係数を求める方法が使われます.
フーリエ級数は,前述のように各周波数成分の線形一次結合によって表されますので,計算機による演算との相性が良いことが知られています.
前述のように,任意の信号は単純な周期関数の重ね合わせにより成り立ちます.各周波数成分がどのくらいの強さで含まれているかを表したものがパワースペクトルであり,波の振幅を周波数ごとに分布させたものとなります.ある周期成分の強さ(パワー)Pnは,その周波数における成分の大きさ(絶対値),
Pn = SQRT(an2 + bn2)
と表されます.また,周波数を横軸に,Pnを縦軸にとり,それぞれの周波数成分の大きさをグラフにしたものをパワースペクトルといいます.パワースペクトルは,同じ周波数成分の強さのみを表しているため位相がわかりません.そこで,それぞれの周波数成分の位相を表したものを位相スペクトルといいます.
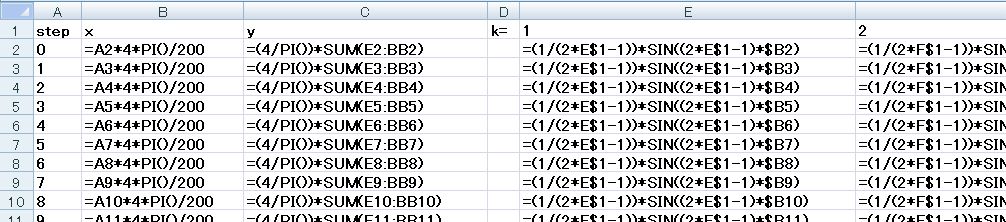
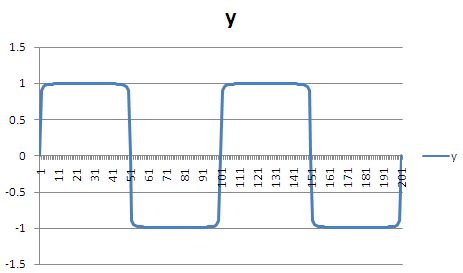
例題4.4
次の式は,方形波をフーリエ級数展開したものである.
y = (4/π) { sin(x) + (1/3) sin(3x) + (1/5) sin(5x) + (1/7) sin(7x) + … }
= (4/π) ∑ { ( 1/(2k - 1) ) sin( (2k - 1)・x ) } (k = 1~∞)
k = 1~50,0 ≦ x ≦ 4πとし,方形波を近似しなさい.
ヒント:
入力式の例
(1) 1行目に見出し(step, x, y),および,kの値を《連続データの作成》で1~50まで行方向に入力します(E1~BB1まで入力されます).
(2) 三角関数のデータ入力の要領で,A, B列に0~4πのxのデータを作ります(ここでは,0~4πを200分割しています).
(3) E2のセルに漸化式 ( 1/(2k - 1) ) sin( (2k - 1)x ) を入力します.コピーしたときの参照位置に注意して,複合参照を使います.
(4) E2のセルをBB2まで右方向にコピーします.
(5) E2~BB2までのセルを選択し,202行目までコピーします.
(6) C列にフーリエ級数の式を入力します.
(7) C列を選択してグラフを作成します.
(8) 2周期分の方形波のグラフが表示されます.
データは,BB列202行まであります.
演習4.4(解答例)
(1) 次の式は,のこぎり波をフーリエ級数展開したものである.
y = (2/π) { sin(x) + (1/2) sin(2x) + (1/3) sin(3x) + … }
= (2/π) ∑ { (1/k) sin(kx) } (k = 1~∞)
k = 1~50,0 ≦ x ≦ 4πとし,のこぎり波を近似しなさい.
(2) 次の式は,デルタ関数をフーリエ級数で近似したものである.
y = cos(x) + cos(2x) + cos(3x) + …
= ∑ cos(kx) (k = 1~n)
k = 1~50,0 ≦ x ≦ 4πとし,デルタ関数の近似波形を表示しなさい.
ここでは CR 微分回路の過渡現象を数値計算によってシミュレートします.
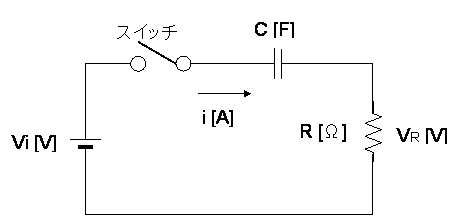
この回路の方程式は,次のように表されます.
Vi = R・i + (1 / C)・∫ i dt
これを,電流について変形すると
i = (1/R)・(Vi - (1 / C)・∫ i dt
となります.上式の積分項は,区分求積法などの漸化式に置き換えられますので,
in+1 = (1/R)・( Vi - (1 / C)・(in + in-1 ))
と表されます.また,回路の出力は電圧VR であり,
VR = R * i
によって求められます.この各変数および式を表計算ソフトに作ることで,CR 微分回路の過渡現象をシミュレートできます.
例題4.5 CR 微分回路の過渡現象シミュレーション
上式より,RC直列回路の過渡現象をシミュレートしなさい.
ただし,R = 20,C = 20 ,Vi はステップ入力(Vi = 1 (t > 0)) とし,t = 2000まで計算しなさい.
ヒント:
次のような式を入力して確認してください.式の意味については各自考察してください.
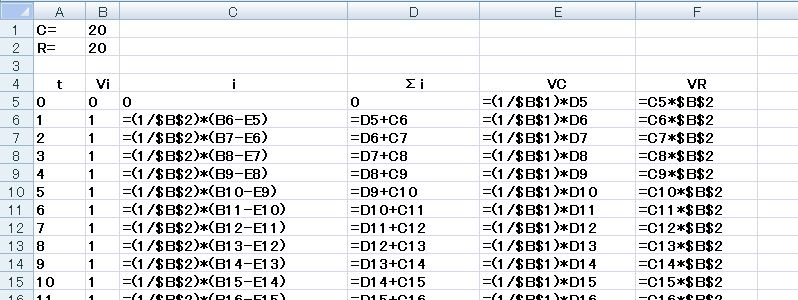
演習4.5 RC積分回路の過渡現象シミュレーション(解答例)
(1) 例題を参考に,RC 積分回路について過渡現象をシミュレートしなさい.
ただし,R = 10,C = 30 とし,Vi はステップ入力(Vi = 1 (t > 0)) とし,t = 2000まで計算しなさい.
(2) 入力電圧を傾斜関数
(Vn+1 = Vn + 0.01)
とした場合の回路の挙動を確かめなさい.
(3) 入力電圧を交流(正弦波)を入力した場合の回路の挙動を確かめなさい.
ただし,t = 0~2000において,10周期の正弦波を入力すること.
カオスとは,ある時点での状態(初期値)が与えられれば,その後の挙動が全て決まるような決定論的法則に則ったシステムでありながら,不規則かつ不安定な挙動をして未来の状態が予測不可能な現象です.
数学的解析は可能ですが,漸化式で数値計算を行うと不規則な挙動を示すのが,カオスの原点とも言うべきロジスティック写像と呼ばれる次のような漸化式です.
xn+1 = axn ( 1 - xn ) (0 ≦ x ≦ 1)
この式は,xn の値が決まれば,次の xn+1 の値が決定します.つまり,初期値が与えられれば,全ての xn が決まるわけですが,その値の振る舞いは不規則なものとなります.
演習4.6 カオス現象の計算(解答例)
(1) 次の手順を参考に,上記ロジスティック写像を表計算ソフトで実行しなさい.
① A1 に,【x0 =】と入力し,b1に x の初期値【 0.2 】を入力する.
② A2:A401 に,a の値として 0.01 ~ 4.00 を 0.01刻みで入力する.
③ B2 に【 = $A2 * $B$1 * ( 1 - $B$1 ) 】を入力する.
④ C2 に【 = $A2 * B2 * ( 1 - B2) 】を入力する.
⑤ C2 を AZ2 まで右方向にコピーする.
⑥ B2:AZ401 を選択し,B2:AZ2 を下方向へコピーする.
⑦ AA2:AZ401 を選択し,折れ線グラフで表示する.
(2) 初期値を変えて,カオスの挙動を確かめなさい.
(3) 3 ≦ a ≦ 4 の範囲でグラフを表示しなさい.