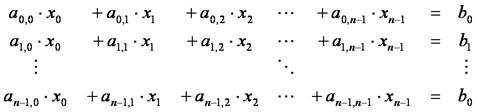
ここでは，数値計算法の復習とプログラミング練習を兼ねて，以前行った微分・積分と非線形方程式の根を数値計算で求めるJavaプログラムを作成します．また，新たに線形方程式や常微分方程式の数値解法について取り上げます．
gnuplotは，簡単なコマンドを使って対話的に2次元や3次元のグラフを表示することができる便利なツールです．使い方の詳細などについては，Webサイトや参考書などを参照してください．
(1) gnuplotのダウンロードサイトからリンクを辿り，最新版のファイルをダウンロードし，適当なフォルダに解凍する．
(2) wgnuplot.exeを実行し，gnuplotのウインドウを開く．
(3) フォントが小さいので，ウインドウ上で右クリックし，Choose Fontで見やすいフォントとサイズに変更する．
(4) 同様に右クリックし，Update wgnuplot.iniで変更を保存する．
ここでは，gnuplotの簡単な使い方を説明します．
plot … データファイルや関数を描画
plot sin(x) w l … sin(x)のライン描画
plot "data.txt" u 1 … data.txtの1列目のデータを描画
replot… 再描画，重ねて描画
replot cos(x) … 前のグラフにcos(x)を重ねて再描画
set … 設定
set xrange[-20:20] … x軸の範囲を-20～+20に設定
cd … ディレクトリ(フォルダ）の移動．ディレクトリ名はシングルクオーテーションで指定．
cd '\work' … C:\workディレクトリに移動
微分の項を参照
補足： Mathクラスについて
Mathクラスは，数学計算のためのフィールドやメソッドを提供します．各フィールドやメソッドの詳細は，JDK SEのドキュメントのMathクラスなどを参照してください（ただし，各自のJavaのversionに合わせたドキュメントを参照のこと）．
Mathクラスのフィールド例
| フィールド名 | 内容 | 使用方法 |
| PI | πにもっとも近い double 値 | Math.PI |
Mathクラスのメソッド例
| メソッド名 | 動作 | 使用方法 | 意味 | 戻り値，引数 |
| abs() | 各型の絶対値を返す | a = Math.abs(b) | a = |b| | すべての型に対応． ただし，戻り値と引数の型は同じ． |
| max() | ２つの引数の最大値を返す | c = Math.max(a, b) | a, bの大きいほうをcに代入 | すべての型に対応． ただし，戻り値と引数の型は同じ． |
| min() | ２つの引数の最小値を返す | c = Math.min(a, b) | a, bの小さいほうをcに代入 | すべての型に対応． ただし，戻り値と引数の型は同じ． |
| pow() | べき乗を返す | z = Math.pow(x, y) | z = xy | 戻り値，引数ともにdouble型 |
| sqrt() | 平方根を返す | z = Math.sqrt(x) | z = √x | 戻り値，引数ともにdouble型 |
| exp() | 指数関数を返す | z = Math.exp(x) | z = ex | 戻り値，引数ともにdouble型 |
| log() | 自然対数を返す | z = Math.log(x) | z = logex | 戻り値，引数ともにdouble型 |
| log10() | 常用対数を返す | z = Math.log10(x) | z = log10x | 戻り値，引数ともにdouble型 |
| sin() | 指定された角度の正弦を返す | z = Math.sin(x) | z = sin(x) | 戻り値，引数ともにdouble型 |
| cos() | 指定された角度の余弦を返す | z = Math.cos(x) | z = cos(x) | 戻り値，引数ともにdouble型 |
| tan() | 指定された角度の正接を返す | z = Math.tan(x) | z = tan(x) | 戻り値，引数ともにdouble型 |
例題6.1 （サンプルプログラム: Differential.java）
二次関数 y = x2の導関数を求めるプログラムを差分商を用いて作り，コンパイル・実行しなさい．また，gnuplotにてグラフ化し，y = 2x のグラフと比較しなさい．ただし，xの区間を[0, 5]とし，100分割すること．
ヒント：
・関数f(x)の差分商は，(f(x+h)-f(x))/hで表される．
・関数, 導関数の値をスペース区切りでファイルへ書き込む．
・gnuplotでは，次のようにしてファイルの中の各列を表示できる．
plot "ファイル名" u 1,"ファイル名" u 2,…
また，例えば，ファイルの1列目と2列目の関係を表示するには，
plot "ファイル名" u 1:2
とする．
・関数f(x)の2階の差分商は，次の式で表わされる．
{f(x+2h) - f(x+h)}-{f(x+h) - f(x)} / h2
演習6.1（解答例： Differential1.java）
関数 ex の導関数を数値計算によって求めるプログラムを作り，ex と一緒にグラフ表示せよ．ただし，xの区間を[0, 1]とし，それを100分割するものとする．また，同様に，ex の2階の導関数も求め，併せてグラフ表示せよ．
演習6.2（解答例： Differential2.java）
関数sin(x)の導関数を数値計算によって求めるプログラムを作り，sin(x)と一緒にグラフ表示せよ．ただし，xの範囲は，0～2πとし，それを100分割するものとする．また，同様に，sin(x)の2階の導関数，3階の導関数も求め，グラフ表示せよ．
積分の項を参照
例題6.2 （サンプルプログラム: Integration.java）
f(x) = xの区間[0,1]の積分を，区分求積法，中点法それぞれによって求めるプログラムを次の条件で作りなさい．
(1) xの区間を10分割する．
(2) xの区間を100分割する．
演習6.3 （解答例: Integration.java）
例題6.2のプログラムに台形法によって積分値を求め表示する命令を追加しなさい．ただし，xの範囲は[0, 1]とし，それを100分割するものとする．
演習6.4 （解答例: Integration1.java）
f(x) = sin(x)の積分を区分求積法，中点法，台形法それぞれによって求めるプログラムを作りなさい．ただし，xの範囲は，0～πとし，それを100分割するものとする．
演習6.5 （解答例: Integration2.java）
単位円の方程式の区間[0, 1]の面積を，区分求積法，中点法，台形法それぞれによって求めて4倍し，単位円の面積を求めなさい．ただし，xの区間を100分割するものとする．
非線形方程式の根の項を参照
補足： 収束判定について
(1) 計算機イプシロン
計算機の中で，1+ε > 1 が成立する最小の正数εを計算機イプシロンといい，εで表します．この値は，反復計算時の収束判定や，微分積分のステップ幅などの目安として使われます．なお，C言語では，float.hの中に FLT_EPSILON，DBL_EPSILON が定義されています．
(2) 2分法の収束判定
2分法における収束判定には，区間[a, b]において，
① |b - a| < ε
② |f(c)| < ε
とする方法がある．
①の場合，収束するための反復回数を
|b - a| / 2n < ε
より
n > {log(|b - a|/ε)} / log2
と予め求めることができる．
(3) ニュートン法，割線法などの収束判定条件
ニュートン法，割線法などにおける収束判定条件には，
① 許容誤差： |xn+1 - xn| < ε
② 許容相対誤差|(xn+1 - xn) / xn| < ε
③ 許容残差： |f(xn+1) - f(xn)| < ε
などがあるが，f'(xn)の値，つまり，xnにおける接線の傾きが大きいと，①や②の条件が満たされてしまうことがある．③を使うと，その危険性は少ないが，必ずしも根の近くで収束するとは限らない．
例題6.3 （サンプルプログラム: NonlinearEquation.java）
f(x) = x2 - 3 の根を2分法を使って求めるプログラムを作りたい．ただし，2分法はそれぞれメソッドとして作成して，メインメソッドから呼び出すものとする．サンプルプログラムを完成させなさい．また，ε = 10-5とする．
演習6.6 （サンプルプログラム: NonlinearEquation2.java），（解答例: NonlinearEquation2.java）
f(x) = x2 - 5 の根を2分法，ニュートン法，割線法を使って求めるプログラムを作りたい．ただし，2分法，ニュートン法，割線法はそれぞれメソッドとして作成して，メインメソッドから呼び出すものとする．サンプルプログラムを完成させなさい．また，ε = 10-5とする．
演習6.7 （解答例: NonlinearEquatio3.java）
サンプルプログラムを変更し，f(x) = x2 + x - 6 の根( > 0 )を2分法，ニュートン法，割線法を使って求めるプログラムを作りなさい．ただし，ただし，区間の初期値は，[0, 5] ，ε = 10-5とする．
n元の連立一次方程式
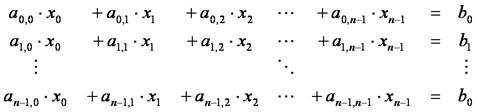
の一般的な解法について説明します．
上式は，行列とベクトルの表記を用いて，
と表すことができます．ここで，Aは，n×nの正方行列で係数行列と呼ばれ，xは求める未知ベクトル(解ベクトル)，bは既知ベクトルです．
このようなn元連立一次方程式の数値解法には
直接法： 式の変形によって解く方法
・ Gaussの消去法
・ Gauss-Jordan法（掃き出し法）
・ 三角化分解法（LU分解法）
反復法： 解に収束する数列を作り出して近似解を求める方法
・ Jacobi法
・ Gauss-Seidel法
などがありますが，ここでは，基本的なGaussの消去法と後の逆行列計算に利用するGauss-Jordan法について説明します．
Gaussの消去法は，筆算で行うように，式を変形させて各変数を消去していく方法です．具体的には，次のようにします．
上記 n元連立方程式において，第1行目の式の両辺をa0,0(≠0)で割り，x0の係数を1とします．このとき，両辺を割る係数（この場合a0,0）をピボットといいます．
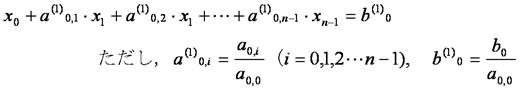･･･(1')
(1')式をa10倍して第2行目の式から引き，第2行目の式から変数x0の項を消去します．以下，同様に，第3～n行目までの変数x0の項を消去します．
次に，x0の項を消去した新しい第2行目の式の両辺をa(1)11(ただし，a(1)11=a(1)01 * a10で割り，変数x1の係数を1として，これを使って第3～n行目の式の変数x1の項を消去します．
以下，同様に，x2～xn-1の項を消去していくと，最終的に次式が得られます．
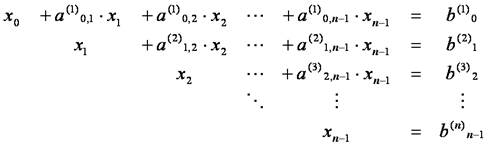
このように，式を変形し変数xi(i = 0～n)を消去していくことを「前進消去」といいます．これは，係数行列Aを次のように上三角行列にする操作となります．
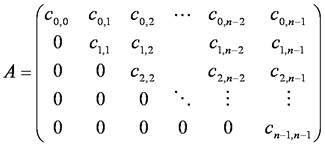
これにより，n行目の式からxn-1が求まります．この解をn-1行目の式に代入すると，xn-2が求まります．このxn-2とxn-1をn-2行目の式に代入すると，xn-3が求まります．以下同様に，n-2行目からさかのぼり，求まった解を順次代入していくことで，全ての解が求まります．これを後退代入といいます．
解法の具体例として，次の3元連立一次方程式をGaussの消去法に則って解いてみます．
3x + 10y - 4z = 11 ･･･(1)
x + 2y + 3z = 14 ･･･(2)
-2x - 4y + z = - 7 ･･･(3)
【前進消去】
第1段階
(1)式の両辺を3で割ってxの係数を1にする．
x + (10/3)y - (4/3)z = 11/3 ･･･(1')
(2)式から(1')式を引く．
0x - (4/3)y + (13/3)z = 31/3 ･･･(2')
(3)式から(1')式の-2倍を引く．
0x + (8/3)y - (5/3)z = 1/3 ･･･(3')
第2段階
(2')式の両辺を(-4/3)で割ってyの係数を1にする．
0x + y - (13/4)z = -31/4 ･･･(2'')
(3')式から(2')式の(8/3)倍を引く．
0x + 0y + (21/3)z = 63/3 ･･･(3'')
第n段階
(3'')式からzの値を求める．
7z = 21 ⇒ z = 3
【後退代入】
得られたzを(2'')式に代入してyを求める．
y - (13/4)*3 = -31/4 ⇒ y = 2
得られたyおよびzを(1')式に代入してxを求める．
x + (10/3)*2 - (4/3)*3 = 11/3 ⇒ x = 1
例題6.4（ サンプルプログラム: LinearEquationSolver.java （線形計算法のクラス．Gaussの消去法メソッドを作成．）， LinearEquationCalculation.java （実行クラス） ）
Gaussの消去法をメソッドとして持つ，n元の連立一次方程式を求める線形計算解法クラスを作りなさい．また，次の連立1次方程式を解く実行プログラムを作成して，解を求めなさい．
3x + 10y - 4z = 11
x + 2y + 3z = 14
-2x - 4y + z = - 7
ここに示したメソッドは，基本的なアルゴリズムであり，ある行のピボットが0の場合は，計算ができなくなります．そのため，ピボットが0であるか判断し，0の場合は，ピボットが0でない行の式，もしくは，変数と順序を入れ替えるなどの処理を行う必要があります．これをピボット選択といいます．
演習6.8
例題6.4のサンプルプログラムをコンパイル，実行し，実行結果とソースファイルを比較しながら理解を深めなさい．．
演習6.9（ 解答例: LinearEquationCalculation.java（実行クラス） ）
例題6.4のクラスを利用して次の連立1次方程式を解くプログラムを作成し，解を求めなさい．
x0 - 2x1 + x2 - 3x3 = -12
2x0 + x1 + 3x2 + 2x3 = 21
x0 + 3x1 - 2x2 + x3 = 5
3x0 + 2x1 + x2 + x3 = 14
Gauss-Jordan法は，前進消去のみで，後退代入を行わないのが特徴です．
Gaussの消去法では，n次連立方程式の第i行目(i = 1～n)の式を変形し，i+1行目以降の式から第i項の変数を消去しましたが，Gauss-Jordan法では，第i行目の式を変形した後，その式を使って，i行目以外の式，つまり，1～i-1行目，i+1～n行目の全ての式から第i項の変数xiを消去します．したがって，第n行の式を変形して他の式から第n項の変数を消去すると，全ての変数の解が求まることになります．
n次連立方程式
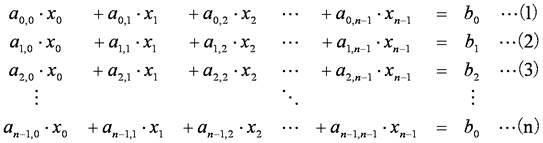
において，(1)式の両辺をピボットa0,0≠0で割り，x0の係数を1とします．
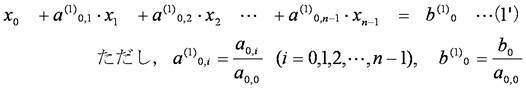
(1')式を使って，第2～n行目の式から変数x0の項を消去します．
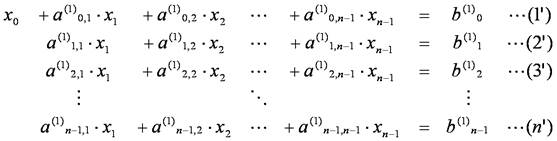
次に，(2')式，つまり，x0の項を消去した新しい第2行目の式の両辺をa(1)1,1（ただし，a(1)1,1=a(1)0,1 * a1,0）で割り，変数x1の係数を1として，これを使って第2行目以外の式の変数x1の項を消去します．
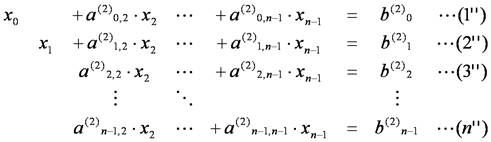
以下，同様に，x2～xn-1の項を消去していくと，最終的に全ての変数の解が得られます．
これは，前進消去を使って，係数行列Aを単位行列にする操作となります．
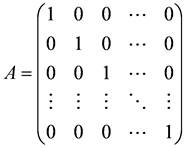
Gauss-Jordan法の手順を用いて，演習6.4(1)の3次連立一次方程式の解を求めよ．
3次の連立方程式
3x + 10y - 4z = 11 ･･･(1)
x + 2y + 3z = 14 ･･･(2)
-2x - 4y + z = -7 ･･･(3)
の解ををGauss-Jordan法により求める．
第1段階
(1)式の両辺を3で割ってxの係数を1にする．
x + (10/3)y - (4/3)z = 11/3 ･･･(1')
(2)式から(1')式を引く．
0x - (4/3)y + (13/3)z = 31/3 ･･･(2')
(3)式から(1')式の-2倍を引く．
0x + (8/3)y - (5/3)z = 1/3 ･･･(3')
第2段階
(2')式の両辺を(-4/3)で割ってyの係数を1にする．
0x + y - (13/4)z = -31/4 ･･･(2'')
(1')式から(2'')式の(10/3)倍を引く．
x + 0y + (57/6)z = 177/6 ･･･(1'')
(3')式から(2'')式の(8/3)倍を引く．
0x + 0y + (21/3)z = 63/3 ･･･(3'')
第3段階
(3'')式の両辺を(21/3)で割ってzの係数を1にする．
0x + 0y + z = 3 ･･･(3''')
(1'')式から(3''')式の(57/6)倍を引く．
x + 0y + 0z = 1 ･･･(1''')
(2'')式から(3''')式の(-13/4)倍を引く．
0x + y + 0z = 2 ･･･(2''')
よって，x = 1, y = 2, z = 3．
以上，前進消去のみで解が求まる．
例題6.5（ サンプルプログラム: LinearEquationSolver2.java（Gauss-Jordan法を追加），LinearEquationCalculation2.java（実行クラス） ）
例題6.4で作成した線形計算解法クラスにGauss-Jordan法を行うメソッドを追加しなさい．また，Gauss-Jordan法のメソッドを使って次の連立1次方程式を解く実行プログラムを作成して，解を求めなさい．
3x + 10y - 4z = 11
x + 2y + 3z = 14
-2x - 4y + z = - 7
Gauss-Jordan法では，Gaussの消去法のメソッドで“k+1行目以降の計算”となっている箇所がk行以外の計算となるため，for文の条件が変わります．また，前進消去の計算過程で既知ベクトルが上書きされ，すべての計算が終了したときの既知ベクトルが最終的な解となるため，未知ベクトルの定義・代入，および，後退代入の部分が必要なくなります．（ただし，クラス全体のコンストラクタとしては，Gaussの消去法で未知ベクトルを使うため定義しています．）
演習6.10
例題6.5のサンプルプログラムをコンパイル，実行し，実行結果とソースファイルを比較しながら理解を深めなさい．．
演習6.11（ 解答例: LinearEquationCalculation2.java（実行クラス） ）
例題6.5のクラスを利用して，演習6.9の連立1次方程式を解くプログラムを作成し，解を求めなさい．
n次の正方行列Aの逆行列A-1とは，AA-1 = A-1A = I（Iは単位行列）を満たす行列のことです．これは，連立方程式の行列表現
において，x=A-1，b=Iと置いたものに他なりません．したがって，逆行列A-1を，前述のGauss-Jordan法を用いて簡単に求めることができます．いま，
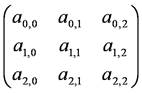
の逆行列A-1をGauss-Jordan法で求めることとします．
まず，元の行列Aの右側に単位行列を並べ，Aの付加行列を作ります．
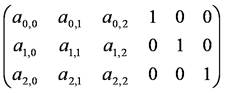
次に，消去の第1段階として，第1行目をa0,0で割ります．
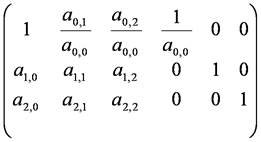
第1行目のa1,0倍を第2行目から，a2,0倍を第3行目から引き，第1列目の要素を消去します．
= 
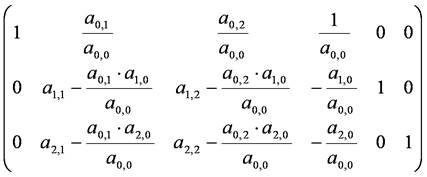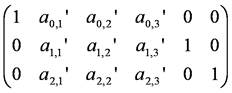
式の簡略化のために，上のように置き，第2段階の消去を行います．第2行目をa1,1'で割り，そのa0,1'倍を第1行目から，a2,1'倍を第3行目から引きます．
= 
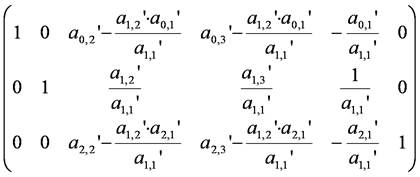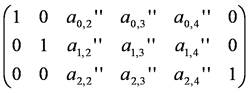
同様に，上のように置き，第3段階の消去を行います．すなわち，第3行目をa2,2''倍で割り，そのa0,2''倍を第1行目から，また，a1,2''倍を第2行目から引きます．
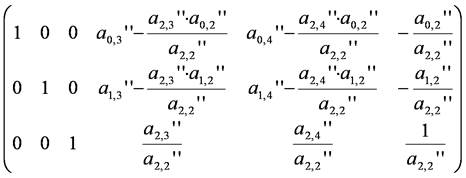
これで，左半分が単位行列となり，右半分が逆行列となります．
Gauss-Jordan法の手順を用いて，逆行列を求める．
3次の正方行列
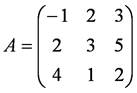
の解ををGauss-Jordan法により求める．
Aの右側に単位行列を並べた付加行列を作る．
第1段階
1行目を-1で割り，その2倍を2行目から，4倍を3行目から引く．
第2段階
2行目を7で割り，その-2倍を1行目から，9倍を3行目から引く．
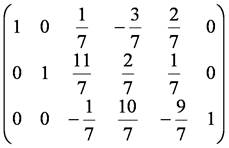
第3段階
3行目を(-1/7)倍で割り，その(1/7)倍を1行目から，(11/7)倍を2行目から引く．
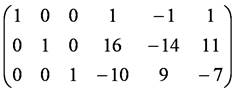
これより，逆行列A-1は，
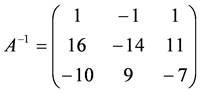
例題6.6（ サンプルプログラム: LinearEquationSolver3.java（逆行列計算を追加），LinearEquationCalculation3.java（実行クラス） ）
例題6.4の線形計算解法クラスに，Gauss-Jordan法を元にした逆行列計算を行うメソッドを追加しなさい．また，次の行列の逆行列を求める実行プログラムを作成して，解を求めなさい．
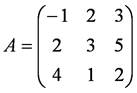
逆行列計算では，Gauss-Jordan法の計算過程で係数行列が上書きされ，すべての計算が終了したときの係数行列が求める逆行列となるため，既知ベクトルの計算に関わる部分が必要なくなります．（ただし，それらは他のメソッドでは使うため，クラス全体のコンストラクタでは定義しています．）
演習6.12
例題6.6のサンプルプログラムをコンパイル，実行し，実行結果とソースファイルを比較しながら理解を深めなさい．
物理的な現象などを表す数学的なモデルとして，常微分方程式がよく用いられます．しかし，複雑な常微分方程式は，解を求めるのが困難であるため，数値計算によって近似解を求める方法が有用となります．
ここでは，常微分方程式の数値解法の基礎となる考え方としてオイラー法を説明し，常微分方程式の代表的な数値解法である4次のルンゲ･クッタ法を紹介します．
の形で表される式を常微分方程式といいます．例えば，
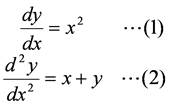
などは常微分方程式です．常微分方程式は，導関数の次数nによって，n階の常微分方程式と呼ばれます．(2)式は，2階の常微分方程式です．
常微分方程式
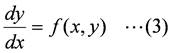
を積分すると，
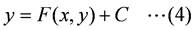
が得られます．(4)式を，(3)式の一般解といい，積分定数Cを設定したものを特殊解といいます．Cは，常微分方程式の初期値(x0, y0)が与えられると決定するため，これを初期値問題といいます．
(1)式を積分すると，一般解
が得られる．今，初期値(x0, y0) = (0, 1)が与えられたとすると，
C = 1となり，特殊解は，
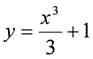
と求まる．
常微分方程式の数値解法では初期値問題を扱い，与えられた初期値に基づいて計算を進めていきます．
常微分方程式dy/dx = f(x, y)は，微小区間の変化率と関数値の関係を表したものです．したがって，初期値(x0, y(x0))から始めて，微小区間h進んだ次の値(x1, y(x1)) = (x0+h, y(x0+h))を順次計算することで，近似解を求めることができます．
このような処理を行うために，1階の微分方程式をすでに見てきたように
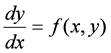
の形に変形する必要があり，これを1階微分方程式の正規形といいます．
高階の微分方程式
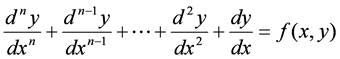
の場合には，最高階の項について解いて，
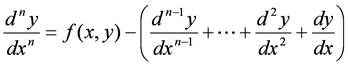
とし，各項の初期値から
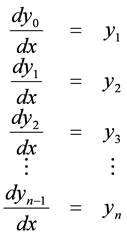
のように低階の値を別の変数として順次求め，その値を用いて
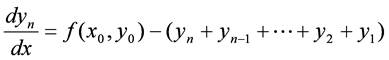
のように求めます．
微分方程式
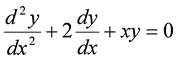
の正規形は，
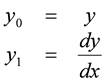
とおくと，
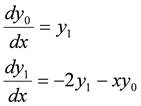
と表せる．
オイラー法は，初期値問題の比較的簡単な数値解法です．初期値(x0, y0)と区分幅hが与えられたとき，初期値から始めて近似式
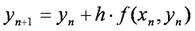
を漸化式として順次計算をしていく方法です．
常微分方程式
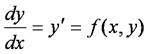
において，点(xn, yn)と区分幅hが与えられたとき，次点の近似値yn+1をテイラー展開によって
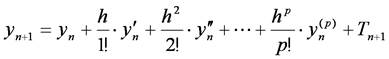
と求めます．ここで，
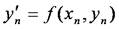
なので，上式は，
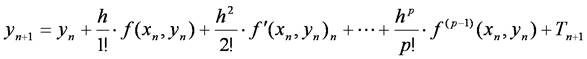
となります．
この式で，p = 1の項（右辺第2項）まで計算し，右辺第3項以上の項を省略すると，オイラー法の近似式
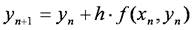
が得られます．また，p = 2の項（右辺第3項）まで計算して右辺第4項以上の項を省略し，
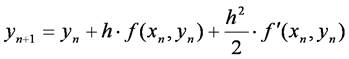
として精度を上げたものを修正オイラー法といいます．
また，別の考え方として，オイラー法の近似式の意味を次のように捉えることもできます．
いま，常微分方程式
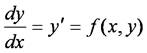
において，点(xn, yn)と十分小さい区分幅 h = xn+1 - xn が与えられたとき，微分の定義を考えると，
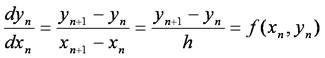
とすることができます．この式をyn+1について解くと，
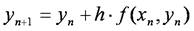
が得られます．
例題6.7（ サンプルプログラム: DifferentialEquationSolver.java（微分方程式の解法クラス），DifferentialEquationCalculation.java（実行クラス） ）
微分方程式
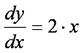
をオイラー法の近似式で表わしなさい．また，上式をオイラー法で計算するプログラムを作り，計算結果をグラフで確認しなさい．ただし，初期値(x0, y0) = (0, 0)，区間幅h = 0.1とし，計算区間を[0, 2]とする．
与式をオイラー法の近似式で表わすと，
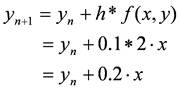
となる．
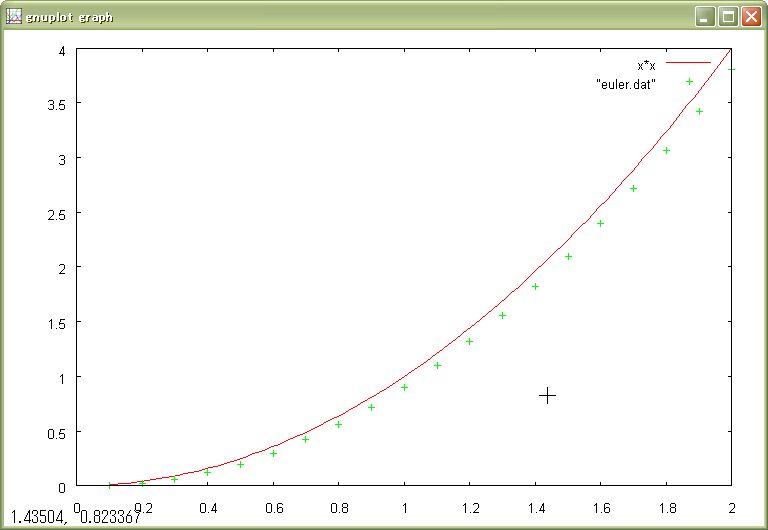
上のサンプルプログラムを実行すると，ファイル"euler.dat"に区間幅毎の(x, y)のデータが書き込まれる．下の図は，微分方程式の解 y = x2と上記プログラムで求めた区間幅毎の近似解をgnuplotで描画したものである．
演習6.14
例題6.7のサンプルプログラムをコンパイル，実行し，実行結果とソースファイルを比較しながら理解を深めなさい．
演習6.15（解答例: DifferentialEquationSolver.java，DifferentialEquationCalculation.java）
(1) 次の常微分方程式を，オイラー法の近似式で表わしなさい．
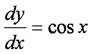
ただし，初期値(x0, y0) = (0, 0)，計算区間を[0, 2π]とし，区分幅をπ/50とする．
(2) 例題6.7のプログラムを修正して，上式を解きなさい．
(3) gnuplotを使って，計算結果と y = sin(x) のグラフとを比較しなさい．
(4) 区分幅をπ/200として計算し，結果を y = sin(x) のグラフと比較しなさい．
演習6.16（解答例: DifferentialEquationSolver2.java，DifferentialEquationCalculation2.java）
(1) 演習6.15の式を修正オイラー法の近似式で表わしなさい．
(2) プログラムに，修正オイラー法を行うメソッド "calculateModifiedEuler" を追加し，区分幅をπ/50として計算した結果を y = sin(x)および演習6.15の結果と比較しなさい．
演習6.17（解答例: DifferentialEquationSolver3.java，DifferentialEquationCalculation3.java）
(1) 次の常微分方程式をオイラー法，修正オイラー法で表わしなさい．
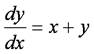
ただし，初期値(x0, y0) = (0, 0)，計算区間を[0, 20]とし，区間を100分割するものとする．
(2) 演習6.16で作成したプログラムのオイラー法および修正オイラー法のメソッドを用いて上式を計算し，y = ex-x-1 のグラフと比較しなさい．
4次のルンゲ・クッタ法は，点(xn, yn)と区分幅hが与えられたとき，次点の近似値yn+1を次式によって求める方法です．
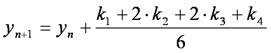
ただし，
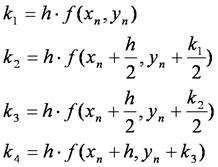
4次のルンゲ・クッタ法では，微小区間hにおける関数の変化を，k1，k2，k3，k4の加重平均として求めることで，精度を上げています. この方法は，オイラー法の区間幅を小さくするよりも効率的で，計算量も少なくなります．上式の証明については別に譲るので，調べてみてください．
例題6.8（サンプルプログラム: DifferentialEquationSolver4.java，DifferentialEquationCalculation4.java）
4次のルンゲ・クッタ法を用いて，微分方程式
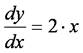
を解け．ただし，初期値(x0, y0) = (0, 0)，区間幅h = 0.1とし，計算区間を[0, 2]とする．
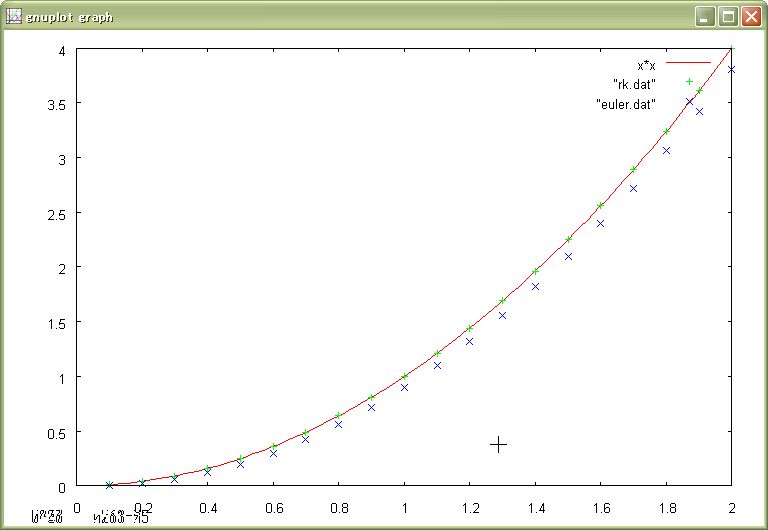
サンプルプログラムをコンパイルしDifferentialEquationCalculation4を実行すると，ファイル"runge_kutta.dat"に区間幅毎の(x, y)のデータが書き込まれる．
下の図は，微分方程式の解y = x2と上記プログラムで求めた区間幅毎の近似解データ"runge_kutta.dat"，および，オイラー法で求めたデータをgnuplotで描画したものである．同じ分解能でもルンゲ･クッタ法のほうが精度の良いデータが求められていることがわかる．
演習6.18
例題6.8のサンプルプログラムをコンパイル，実行し，実行結果とソースファイルを比較しながら理解を深めなさい．
演習6.19（解答例: DifferentialEquationSolver4.java，DifferentialEquationCalculation4.java）
例題6.8のプログラムを修正し，4次のルンゲ・クッタ法を用いて，演習6.15の常微分方程式を計算しなさい．また，gnuplotを使って，計算結果とy = sin(x)のグラフ，および，オイラー法で求めた計算結果とを比較しなさい．
演習6.20（解答例: DifferentialEquationSolver5.java，DifferentialEquationCalculation5.java）
例題6.8のプログラムを修正し，4次のルンゲ・クッタ法を用いて，演習6.17の常微分方程式を計算しなさい．また，gnuplotを使って，計算結果とy = ex-x-1 のグラフと比較しなさい．
